Постановка задачи

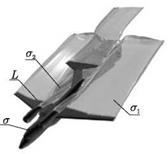
Рассматривается нестационарное обтекание летательного аппарата (ЛА) потоком идеальной несжимаемой жидкости со скоростью Wж (рис. 2.1) Движение ЛА, а также отклонение органов управления и механизации совершаются по произвольным законам. Поверхность летательного аппарата считается непроницаемой. Течение жидкости является потенциальным всюду вне летательного аппарата и вихревых следов, возникающих при отрыве потока с заданных ли­ний. Вихревые следы представляют собой тонкие вихревые пелены, т. е. поверхности, на которых имеется разрыв касательной составляющей скорости. При этом линии отрыва потока задаются.

Обозначим а несущие и управ­ляющие жесткие поверхности са­молета, в том числе гондолу дви­гателя, аі — свободную вихревую пелену, сходящую с несущих и управляющих поверхностей, а2 — поверхность струи. Линии схода пелены обозначим L.

С математической точки зрения поставленная задача сводится к отысканию нестационарных полей скоростей W(r, t) и давлений p(lr, t) в принятой системе координат, которые должны удовлетворять следующим условиям и уравнениям.

— Потенциал возмущенных скоростей U(r, t) в каждый момент времени вне поверхностей а, аі и а2 должен удовлетворять

—

На поверхности а должно выполняться условие непротекания

dU —► ^

dU = — w ~W. (2-2)

— На поверхностях вихревого следа аі и а2, являющихся поверх­ностями тангенциального разрыва, должно выполняться условие отсутствия перепада давления и отсутствия потока жидкости через эту поверхность

Р+ = p-, w+ = W — = Vn, (2.3)

где Vn — нормальная составляющая скорости на поверхности аі.

— На линиях отрыва должно соблюдаться условие Чаплыгина-Жу­ковского о конечности скорости

Wn(W, t) w 0. (2.4)

— На бесконечности возмущения затухают:

AU w 0 при W wix. (2.5)

— Для связи скорости и давления используем уравнение Бернулли

При решении поставленной задачи потенциал U( r, t) или U(M, t) будем искать в виде потенциала двойного слоя:

где gi (M, t) — плотность потенциала двойного слоя, расположенного на поверхности а. При этом скорость жидкости в каждой точке, не лежащей на поверхностях а, аі и а2, определяется формулой

Выражение (2.8) справедливо и на поверхностях а, аі и а2, если входящие в него интегралы понимать как гиперсингулярные в смысле конечного значения по Адамару. Напомним, что потенциал двойного слоя претерпевает скачок на поверхностях, где он размещен, а его нормальная производная непрерывна. Соответственно поле скоростей имеет скачок тангенциальной составляющей на поверхностях лета­тельного аппарата и его следа, а нормальная составляющая на этих поверхностях непрерывна.

Для удовлетворения условия (2.3) будем искать такое решение, в котором поверхности 0 (t) и 02 (t) состоят из точек, движущихся вместе с жидкостью, и плотность потенциала двойного слоя gi(M, t) в каждой такой точке не зависит от времени. Предположим, что в каж­дый момент т ^ t с каждой точки линии схода пелены M(s), где s — длина дуги на этой линии, сходит в поток частица жидкости, которая в момент времени t занимает положение M(s, т, t), и что в каждый момент t совокупность всех точек M(s, т, t) образует поверхность вихревых следов 0 (t) и 02 (t). При этом уравнение движения этих поверхностей принимает вид

dr (sQtт, ^ = W(M(s, т, t), t), т < t, s : M(s) Є L (2.9)

при начальных условиях

W(s, т, t) t=T = WM(s) , (2.10)

где r (s, т, t) и r m (s) —радиус-векторы точек M (s, т, t) и M (s) соот­ветственно, а для функции g2(M, t) справедливо соотношение

g2(M(s, т, t), t) = g2(s, т), т ^ t, s : M(s) Є L. (2.11)

Условие (2.2) эквивалентно уравнению

где f(Mo) = — W^W(Mo).

Наконец, взаимосвязь функций g1 (M, t) и g2 (s, t) описывается еле — дующим соотношением, вытекающим из требования интегрируемости поля скоростей:

g2 (s, t) = g1 (M(s), t, s : M(s) Є L). (2.13)

Таким образом, задача нестационарного отрывного обтекания ЛА идеальной несжимаемой жидкостью свелась к решению замкнутой си­стемы уравнений (2.9)-(2.13) для функций r(s, т, t), g1(M, t), g2(s, т). При этом, если эти функции являются решением указанных уравне­ний, потенциал U(M, t), определяемый формулой (2.7), соответству­ющее ему поле скоростей W(M, t), определяемое выражением (2.8), и давление p(M, t), определяемое из интеграла (2.6), удовлетворяют условиям (2.1)—(2.6).

Схематизацию самолетов осуществляли тонкими пластинами и объ­емными элементами. Крыло и другие несущие поверхности схематизи­ровали тонкими пластинами, изогнутыми по средней линии профилей, а фюзеляж и мотогондолы двигателей — объемными элементами. Пла­стины и элементы моделируются непрерывно распределенным двой­ным слоем особенностей е дискретизацией замкнутыми вихревыми
рамками, В данном случае используются замкнутые вихревые рамки (ячейки) четырехугольной формы, По контуру каждой ячейки i разме­щены вихревые нити, интенсивность которых полагается неизвестной, Вихревые нити индуцируют скорости в соответствии с законом Био — Савара. Общее поле скоростей отыскивают в виде суммы скоростей, индуцируемых всеми вихревыми рамками, моделирующими поверх­ность тела и его след, и скорости набегающего потока:

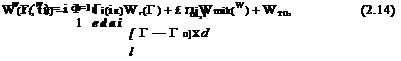N

После этого задача сводится к определению неизвестных интенсив­ностей вихревых рамок, моделирующих тело Гф и вихревой след rm, l, а также координат угловых точек вихревых рамок r m, i. Для определе­ния интенсивностей Г i в каждой вихревой рамке специальным образом выбирается контрольная точка (точка коллокации), для которой запи­сывается условие непротекания тела в этой точке. При этом возникает система линейных алгебраических уравнений, относительно Гі:

N

Y, Fi(tk R, — fk, j = 1…N, (2.15)

і=і

При моделировании вихревого следа предполагается, что вихревые рамки с течением времени движутся вместе с жидкими частицами, а их интенсивности Гтіг при этом остаются постоянными:

r m, l(tk) — r m, l(tk — 1) + ( r m, l(tk — 1), ~tk—)^^t, I < к. (2.17)

В каждый момент времени образуется новая вихревая ячейка, две вершины которой лежат на линии отрыва:

—ki(tk) — — і, (2.18)

а интенсивность вихревой нити на вновь сошедшей рамке определяется через интенсивности вихревых нитей, лежащих на поверхности тела и имеющих с ней общую сторону:

Tm. l —г i+ ™ — Г i — ™. (2.19)

В формулах (2.14)-(2.19) l — номер отрезка на линии отрыва, с кото­рого сошла рамка bm, i, m — время схода рамки в поток.

Таким образом, задача решается по временным шагам до заданного конечного расчетного шага. На каждом расчетном шаге с использова­нием интеграла Коши-Лагранжа вычисляются нагрузки.